TEXSTAN
Institut für Thermodynamik der
Luft- und Raumfahrt - Universität Stuttgart
Mechanical Engineering
- The University of Texas at Austin
- home |
- overview |
- modeling |
- boundary layer |
- pipe flow |
- turbine blade
initial profiles
Initial profiles are used to start the integration in TEXSTAN, and they can either be auto-generated using analytic equations programmed into TEXSTAN or they can be user-supplied profiles, typically from experimental data.
Auto-Generated Profiles - The auto-generated profiles for internal flows use analytical equations that are programmed into TEXSTAN. The three choices are
- flat entry-region profiles for either laminar or turbulent flow (kstart = 1)
- hydrodynamically fully-developed laminar flow profiles (kstart = 2)
- turbulent flow profiles (kstart = 3)
The flat entry-region profiles permit study of hydrodynamically developing flow and, if heat transfer is being considered, the combined entry flow problem where heat transfer also begins at the entrance to the channel. Note that for internal flows, TEXSTAN either computes laminar flow (ktmu is set =0) or turbulent flow (ktmu > 0). However, the only really accurately-modeled combined entry turbulent flow requires a 2-equation turbulence model.
The hydrodynamically fully-developed laminar profiles are designed primarily to study the unheated starting length heat transfer problem, and to examine the effect of Prandtl number on this class of flow. Note that the flow must be constant property. For the circular pipe and a constant surface temperature, the thermally fully-developed flow case can be studied.
The turbulent profile formulation permits the study of turbulence models and how they affect friction and heat transfer for hydrodynamically and thermally fully-developed flow cases. The velocity profile uses the classic law-of-the-wall for the inner region and a power-law formulation for the outer region of the turbulent boundary layer.
There are a set of seven variables that describe the auto-generated profiles for any internal flow. The variables dyi and rate set the y spacing for the velocity profile, which in turn controls the grid (finite difference mesh) for TEXSTAN. These variables have had considerable testing to establish values that yield grid-independent solutions (with respect to the cross-flow direction), and their recommended values are quite reliable. The variable tref establishes the mass-averaged temperature, which is also called the mixed-mean temperature or the mean temperature or the bulk temperature. The two variables tuapp and epsapp are applicable only to turbulent flows to describe the flow entry turbulence intensity and turbulence dissipation. The variable twall establishes the surface temperature of the initial profile.
Flat Profiles for Combined Entry Flow - This option can be used for any internal flow geometry and for any Reynolds number regime, laminar or turbulent. The option generates flat velocity and other dependent variable profiles.
| variable | value | description |
|---|---|---|
| dyi | 5.0E-04 | laminar flow |
| 1.0E-06 | turbulent flow | |
| rate | 0.09 | laminar flow |
| 0.175 | turbulent flow | |
| reyn | ReDh | hydraulic diameter Reynolds number |
| tref | = 0.0 | only momentum equation being solved (neq=1) |
| Tm | mass-averaged temperature | |
| tuapp | = 0.0 | laminar flow (ktmu=0) |
| = 0.0 | turbulent flow with mixing length model | |
| Tu | turbulent flow with 1- and 2-eqn models - Tu (in percent) for computing kinl | |
| epsapp | = 0.0 | laminar flow (ktmu=0) |
| = 0.0 | turbulent flow with mixing length and 1-eqn models | |
| εinl | turbulent flow with 2-eqn model - initial value of turbulence dissipation | |
| =0.0 | turbulent flow with 2-eqn model - TEXSTAN estimates initial value of turbulence dissipation | |
| twall | = 0.0 | only momentum equation being solved (neq=1) |
| Ts | surface temperature, must be same value as tref |
The variables dyi and rate set the y spacing for the velocity profile, where y is measured from the surface. Then for axisymmetric flows with a symmetry line, the y location is transformed into a radial location using r = (rs - y). The same y distribution is used for generating all dependent variables.
The first y location in the grid is y(1)=0, and the second y location is calculated to be y(2))=del99*dyi, where del99 for pipe flow (kgeom=4) is the wall radius, for parallel-plane channel flow (kgeom=5,6) it is the channel half height, and for annular flow (kgeom=7), it is arbitrarily set equal to the average of the inner and outer radius. The next location is power-law expanded (sometimes referred to as a compound interest formulation) to be y(3)=y(2))*(1+rate), and so forth. The expansion is permitted to continue until the value of y exceeds 0.05*del99, and from that location outward, all y values are equally spaced at 0.05*del99. This algorithm is used for both planar and axisymmetric coordinates, and then for the axisymmetric r coordinate in kgeom=4,7 y is linearly transformed such that r=0 becomes the centerline.
With this overall algorithm, there will be a significant number of points near the no-slip surface, depending on the values of both variables. For laminar flow, the suggested variables have been shown to provide grid-independent solutions over the laminar Re range. For Reynolds numbers that permit the flow to go through transition and become fully turbulent, the grid needs to be much finer to insure that once the flow becomes fully turbulent, there will be a significant number of points within the laminar sublayer (y+ ≤ 10 for smooth wall turbulent flows). Again the recommended values for dyi and rate have been tested for grid independent friction and heat transfer results.
With this overall algorithm, there will be a significant number of points near the no-slip surface, depending on the values of dyi and rate. For laminar flow, the suggested values have been shown to provide grid-independent solutions over the laminar Re range. For a flow that starts as an entry flow with a flat profile and transitions to become fully turbulent flow, the grid will need to be much finer to insure that once the flow becomes fully turbulent, there will be a significant number of points within the laminar sublayer (y+ ≤ 10 for smooth wall turbulent flows). Again the recommended values for dyi and rate have been tested for grid independent friction and heat transfer results.
The flow entrance velocity is the mass-averaged value, and it is set using the hydraulic diameter Reynolds number definition
![]()
where the viscosity is evaluated at the entrance temperature, tref, the density is evaluated at tref (and the entrance pressure, po if the density also depends on pressure), and Dh is the hydraulic diameter. Once the flat profile is created the no-slip boundary conditions are applied and the mass flow rate is computed and fixed constant using
![]()
and from this mass flow rate the true Reynolds number for any geometry class of internal flow is then determined
![]()
The choice of specifying an entrance Reynolds number rather than an entrance mass flow rate removes iteration on the value of um when no-slip is accounted for, but it leads to an actual Reynolds number that usually is slightly different from the input reyn value.
Once the mass flow rate is established, the mass-averaged velocity for any location in the solution is computed using
![]()
where the mean density, ρm, is either the input density, rhoc, for kfluid=1, or it is computed at the mass-averaged temperature of the flow, determined from the mass-averaged static enthalpy
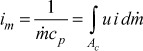
and then converted to the mass-averaged temperature Tm = ƒ(im) from the variable-property tables or functions. Note that for variable property flows, all thermophysical properties are evaluated at the mass-averaged temperature.
Creating flat entrance temperature profiles requires the initial profile variable tref be the same as initial profile variable twall.
To create a flat entrance turbulence kinetic energy profile, the input turbulence level, tuapp (in percent) is converted using
![]()
Extensive testing of entry region flows using various two-equation turbulence models has shown that using tuapp = 10 percent gives realistic behavior for most two-equation models in the entrance region, and for all models, the asymptotic behavior of the friction and heat transfer is found to be independent of tuapp.
To create a flat entrance turbulence dissipation profile, the user can specify epsapp, or if epsapp=0, a model in the initial profile generator will compute an initial value. We can estimate epsapp using either two-equation model ideas or one-equation model ideas. The first estimate comes from the two-equation formulation of the turbulent viscosity
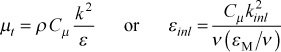
This formulation requires a choice for the ratio of the turbulent to laminar viscosity ratio, (εM / ν), estimated to be on the order of 100 in the entrance region, consistent with the constant diffusivity model for internal flows, described in detail in the modeling: mixing length model section of this website.
A second formulation comes from the development of the modeling: one-equation model section of this website, where the fully turbulent Couette flow region has production equals dissipation, and this leads to
![]()
and with Cd = 0.09 and lm = 0.07δ for channel flows, we find
![]()
Currently TEXSTAN uses the second formulation to estimate the inlet turbulence dissipation, with 0.03δ in the denominator.
Hydrodynamically Fully-Developed Laminar Flow with Heat Transfer - This option provides hydrodynamically fully-developed velocity profiles for the pipe geometry (kgeom=4), the parallel-planes geometry (kgeom=5,6) and the annular geometry (kgeom=7) and constant properties (kfluid=1). This kfluid option has been primarily designed to study the unheated starting length case (thermal entry flow) where the temperature profile is flat (twall=tref).
| variable | value | description |
|---|---|---|
| dyi | 5.0E-04 | |
| rate | 0.09 | |
| reyn | ReDh | hydraulic diameter Reynolds number |
| tref | = 0.0 | only momentum equation being solved (neq=1) |
| Tm | mass-averaged temperature | |
| tuapp | = 0.0 | laminar flow (ktmu=0) |
| epsapp | = 0.0 | laminar flow (ktmu=0) |
| twall | = 0.0 | only momentum equation being solved (neq=1) |
| Ts | surface temperature (if same value as tref, a flat temperature profile is created) |
For the circular pipe of radius rwall,
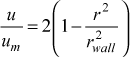
For the parallel-planes channel, where a is the half-height of the channel,
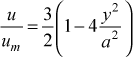
For the annulus, where ri is the inner radius and ro is the outer radius,
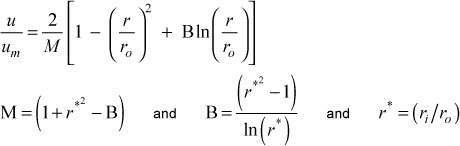
As was noted above, this option for internal flows is not really designed for thermally fully developed temperature profiles, but it is possible by specifying a different value for twall from tref. It is not a correct profile for the constant heat flux boundary condition, and it is only partially tested for parallel planes. It has not developed for the annular geometry.
Turbulent Flow Profiles - This option provides turbulent velocity and thermal profiles for a wall temperature boundary condition, and the temperature profile is approximately correct for a wall heat flux boundary condition.
| variable | value | description |
|---|---|---|
| dyi | 0.1 | interpreted as y+, wall coordinates |
| rate | 0.175 | |
| reyn | ReDh | hydraulic diameter Reynolds number |
| tref | = 0.0 | only momentum equation being solved (neq=1) |
| Tm | mass-averaged temperature | |
| tuapp | = 0.0 | turbulent flow with mixing length model |
| Tu | turbulent flow with 1- and 2-eqn models - Tu (in percent) for computing kinl | |
| epsapp | = 0.0 | turbulent flow with mixing length and 1-eqn models |
| εinl | turbulent flow with 2-eqn model - initial value of turbulence dissipation | |
| =0.0 | turbulent flow with 2-eqn model - TEXSTAN estimates initial value of turbulence dissipation | |
| twall | = 0.0 | only momentum equation being solved (neq=1) |
| Ts | surface temperature, must be same value as tref |
The variables dyi and rate set the y spacing for the velocity profile, where y is measured from the surface. Then for axisymmetric flows with a symmetry line, the y location is transformed into a radial location using r = (rs - y). The same y distribution is used for generating all dependent variables. Note that these definitions are completely different from those used for kstart=1 (flat initial profiles for turbulent entry flow), but the overall procedure for computing the y-distribution remains qualitatively the same.
For developing the grid with turbulent profiles, the grid is first established in wall or plus coordinates, and then converted to physical coordinates. The first y+ location in the grid is =0, and the second y+ location is calculated as y+(2)=dyi. The next location is power-law expanded (sometimes referred to as a compound interest formulation) to be y+(3)=y+(2)*(1+rate), and so forth. The expansion is permitted to continue until the value of y+ exceeds 0.035*δ99+ and from that location outward, all y+ values are equally spaced at 0.035*δ99+. The variable δ99+ = (δ99)/(ν / uτ) is the physical upper limit for y converted to plus coordinates, and δ99 (del99) for pipe flow (kgeom=4) is the wall radius, for parallel-plane channel flow (kgeom=5,6) it is the channel half height, and for annular flow (kgeom=7), it is arbitrarily set equal to the average of the inner and outer radius. This algorithm is used for both planar and axisymmetric coordinates, and then for the axisymmetric r coordinate in kgeom=4,7 y is linearly transformed such that r=0 becomes the centerline.
With this overall algorithm, there will be a significant number of points near the no-slip surface, depending on the values of both variables. The recommended values for dyi and rate have been tested for grid independent friction and heat transfer results. Once the grid is established in plus coordinates, turbulent boundary layer theory and the mixing length turbulence model are used to obtain the velocity and temperature profiles.
For the plus variables with internal flows, the value of the friction velocity, uτ = √(τwall/ρ) = u∞ √(cf /2), is estimated from the friction coefficient correlation cf /2 = [2.236 log(ReDh) - 4.639]-2 which is ok for both the pipe and parallel planes geometry because of the use of the hydraulic diameter Reynolds number. If heat transfer is being considered, to obtain the surface heat flux, we use the Chilton-Colburn-Reynolds analogy to calculate the heat transfer coefficient, StPr2/3 = cf /2 , and the convective rate equation qs" = h(Ts-Tm). The profile for velocity has to extend from the wall to the centerline. The velocity mean value comes from the Reynolds number, and then the centerline velocity is estimated using (um /ucl) = 0.817 . If heat transfer is being considered, (Tm - Ts)/(Tcl - Ts) = 0.817, where Ts = twall and Tm = tref.
The remainder of the analytical development of these profiles is almost identical to that presented in the Turbulent Flow Profiles part of the external flows: initial profiles section of this website, and it is not reprinted here.
User-Supplied Profiles - The primary reason TEXSTAN has auto-generated profiles is that auto-generated profiles yield grid-independent solutions. When user-supplied profiles are chosen as a method to start TEXSTAN, the user may risk not achieving grid independence as described in the overview: numerical accuracy section of this website. The setup for user-supplied profiles mostly follows that described in the corresponding part of the external flows: initial profiles section of this website, and it is not reprinted here.
website updated Sept 2010 © 1996-2010 Michael E. Crawford - all rights reserved - website validated for CSS 2.1 and XHTML 1.0 strict at www.w3.org
