mass transfer

Surface mass transfer is modeled using large mass transfer theory where the mass transfer rate equation is given by m" = g B; m" is the surface mass flux in units of (kg/(m²-s); g is the mass transfer conductance in the same units as m"; and B is the driving force (non-dimensional). This rate equation is analogous to the convective heat transfer rate equation, q" = h  (T_s-T_∞), where the heat flux is proportional to the temperature driving force, and h is the heat transfer conductance (or coefficient). An example of a large mass transfer problem is the wet-bulb psychrometer, and other engineering examples are presented in Chapter 19 of CHMT.

From a fluid mechanics perspective, m" is assumed to be the normal component of the net mass flux vector of a multicomponent mixture at the interface between the boundary layer and the surface where transfer is occurring, and the transport is by the combined processes of convection and diffusion. From an energy balance consideration, the specific enthalpy of each component is transported by both processes, and these terms will contribute in the generalized energy transport equation. In a binary mixture boundary layer there will be only one component at the surface. In large mass transfer problems, g is strongly dependent on the m" via the surface normal velocity component as well as variable properties, in analogy with how h has a strong nonlinear dependence on the near-surface fluid mechanics and variable property effects.

There exists a limiting case for mass transfer when the driving force B approaches zero and the mass transport equation becomes linear, in analogy to the heat transport equation being linear in the absence of variable properties and viscous dissipation. Then the mass transfer driving potential, B, simplifies and the mass transfer conductance is replaced by g^*. This leads to the concept of small mass transfer theory. The simplification of the mass transfer driving force, B, is discussed in detail in Chapter 18 of CHMT.

TEXSTAN is programmed to calculate the small mass transfer problem for a binary mixture boundary layer, where A is the substance being transferred by convection and diffusion, where A might be water vapor (H₂O) evaporating at a low rate into an air boundary layer or naphthalene (C₁₀H₈) evaporating into an air boundary layer. TEXSTAN computes the wall mass flux using Fick's law for diffusional mass transport at the no-slip surface (similar to the procedure of computing the wall heat flux using Fourier's law for diffusional heat transport at the no-slip surface). The convective mass transfer rate equation and the associated nondimensional parameters are given by

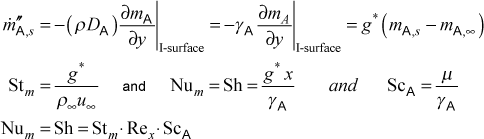
The symbol m_A represents the variable m_j, the mass concentration of component j, defined as (ρ_j /ρ_mix) in units of kg(j)/kg(mix) or lbm(j)/lbm(mix), and it is the dependent variable in the boundary layer mass transfer equation (see overview: transport equations section of this website). Its value at the surface is m_A,s , and this is the TEXSTAN variable cs in the output files. Its value at the free stream is m_A,∞ , and this is the TEXSTAN variable cinf in the output files. The variable m"_A,s is the surface mass flux of A in units of kg/(m²-s) (or) lbm/(ft²-s), and it is the TEXSTAN variable cflux in the output files. The density in Fick's law is the same as the mixture density. The mass transfer conductance, g^*, has units of kg/(m²-s) (or) lbm/(ft²-s), and it is the TEXSTAN variable mtc in the output files. The variable D_j is the mass diffusion coefficient in units of m²/s (or) ft²/s. The nondimensional mass transfer conductance is written in terms of the Sherwood number, and it is the TEXSTAN variable sh in the output files. It is sometimes called the Nusselt number for mass transfer is Nu_m, and both are analogous to the Nusselt number for heat transfer. The other nondimensional mass transfer conductance is written in terms of the mass transfer Stanton number, St_m, analogous to the Stanton number for heat transfer, and it is the TEXSTAN variable stm in the output files. The Schmidt number for m_j is Sc_j, analogous to the Prandtl number for heat transfer.

Note that the mixture density is constant over the boundary layer for vanishing small mass transfer rates, and the variable m_j can be replaced by ρ_j, equivalent to the concentration variable (c_j M_j), where c_j is the molar concentration of j (kilogram-moles per cubic meter, kmol/m³, in SI) and M_j is the molecular weight of j (kilograms per kilogram-moles, kg/kmol, in SI). If the user assumes that ρ_j is the dependent variable in the transport equation for mass transfer, then g^* becomes h_m, a type of mass transfer coefficient in units of m/s (or) ft/s. The h_m variable is typically found in undergraduate heat transfer texts.